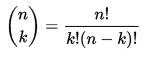The Numbers Game: Shiny and Perfect Pokémon
Find out just how lucky you need to be to find that shiny Pokémon or Pokémon with perfect IVs! Hordes, SOS battles and more are explored as we get mathematical.
The Pokémon games have always involved an element of luck. Previously we’ve covered how luck plays into battling – critical hits, Burn chance, and so forth. Here we now turn to the in-game aspects and turn up the statistics. Many players know the chance of finding a Shiny Pokémon (now) is 1⁄4,096 – but what’s the chance of finding two in a Horde battle? What about the chance of finding a Pokémon with the right Nature, and perfect IVs? And the niche cases such as DexNav Pokémon? We’ll cover as much as we can here on these topics.
Only interested in a particular aspect? Click on a topic below!
- Chance Rates
- Shiny Pokémon
- Pokérus
- Stats
- How we’ll calculate
- Binomial Distribution
- Pascal’s Triangle
- Shiny Charm Rate
- Hordes
- Shiny Soft Resetting
- Masuda Method
- SOS Battles
- The perfect wild Pokémon
Chance Rates
Before we can start calculating for fancy scenarios, we need to consider the stock-standard cases.
Shiny Pokémon
A Shiny Pokémon is simply one that is differently coloured to normal – think say a Pink Butterfree, Red Gyarados or Blue Snover. These were introduced in the generation 2 Pokémon Gold and Silver games, and have featured ever since.
Before generation 6 (that’s Pokémon Gold and Silver all the way to Pokémon Black 2 and White 2), the chance that any typical wild Pokémon you encountered would be a Shiny Pokémon was 1 in 8,192 (or roughly 0.0122%). That’s since changed however. In Pokémon X and Y, and Pokémon Omega Ruby and Alpha Sapphire, the chance is half: 1 in 4,096 (1⁄4,096, or 0.0244%).
There’s additional chance rates below based on the generation six and seven games (ignoring methods like SOS Battles and Horde battles; more on those later):
| Method | Chance for shiny Pokémon |
|---|---|
| Regular | 1⁄4,096 |
| Masuda Method | ~1⁄683 |
| Shiny Charm | ~1⁄1,365 |
| Shiny Charm + Masuda Method | 1⁄512 |
To find out more about these methods and how the games decide whether a Pokémon is shiny (and appearances outside of the games as well), check out the article below!
We won’t consider cases like having a Shiny Charm in the bulk of the article, but if you’re interested in gaining a rough idea, simply divide (or multiply) roughly by a factor of 3 at each relevant step. Emphasis must be placed on the word roughly; check our math section for why.
Pokérus
Pokérus, or Pokémon Virus, is a rare ‘disease’ that Pokémon can catch in the games. Luckily, it doesn’t make them sick; rather, it doubles the Effort Values (or EVs) gained through battles. In layman’s terms, Pokérus quickens the stat gains of Pokémon earned by battling.
So how do you get it? You have to either catch a wild Pokémon with the virus (or hatch a Pokémon with it). The chance is lower than finding a shiny Pokémon however! It is 3 in 65,546; 5.33 times lower than the Shiny chance rate in generation six and seven games. Furthermore, you can’t tell if a Pokémon has Pokérus until you check its status screen or heal it at a Pokémon Centre, so it’s much easier to miss it.
Stats
Lastly, we cover the chance rates for the perfect stat – or rather, an Individual Value (IV) of 31 in generations 3 and onward. IVs apply to each stat from HP to Speed, with 0 being the lowest and 31 the highest. Higher IVs correspond to higher stats!
As there’s 32 values, the chance for an IV of 31 in any one stat in normal cases is 1⁄32. Simple!
There’s also Natures to consider. Natures boost a stat by 10% and lower another by 10%, although five Natures don’t do anything. If you want a specific Nature, the chance of getting that is 1⁄25.
How we’ll calculate

Now that we’re armed with the basic numbers, we’ll discuss how we calculate the probabilities. If you don’t care for mathematics, head onward to the meat of the article!
To begin with, to calculate the probability of two separate events happening, you multiply their own probabilities together. If you want to know the chance of any day being Tuesday and sunny, and the chance of sunshine is, say, 1⁄3, then you multiply the chance of it being Tuesday (1⁄7) with the sunny chance (1⁄3). (1⁄7)*(1⁄3) = 1⁄21. We’ll be using this throughout.
Binomial Distribution
This fancy pair of words isn’t too complex when you get down to it. Binomial features the prefix ‘bi‘ – meaning two – while distribution refers to the range of possibilities. We can use the binomial distribution – or binomial model – to calculate the chance of something happening given two outcomes. This applies to, say, the chance of a coin flip coming up heads or tails, or a Pokémon being Shiny or not.
There’s a formula for the probability (or chance) of events happening that fall into the binomial model, courtesy of Wikipedia:
where:
What does this mean? Well, the simpler terms are as follows. p is the probability of the event we choose (e.g. coin flip giving heads [½]; or a Pokémon being Shiny [1⁄4,096]). n is the number of trials – how many coins do we flip, or Pokémon do we encounter? k is the number of events that occurred – how many heads we get when we flip e.g. n = 10 coins, or how many Shiny Pokémon we see.
The first term with the brackets around an n over k is the binomial coefficient. For those not well versed with maths, the exclamation marks (!) is a factorial – the result of multiplying all numbers below that value until 1. 1! = 1, 2! = 2*1 = 2; 3! = 3*2*1 = 6, 4! = 4*3*2*1 = 24, and so forth.
For sake of example – the chance of flipping one coin and getting heads is ½ (which is our ‘p’). So if we flip a coin thrice (so n = 3), the chance for two heads (k = 2) is calculated through the formula:
(3!⁄(2!*1!)) * (½)2 * (1 – ½)(3-2)
= ((3*2*1)⁄(2*1*1)) * (½)2 * (½)1
= 3 * (¼) * (½)
= 3⁄8
Pascal’s Triangle
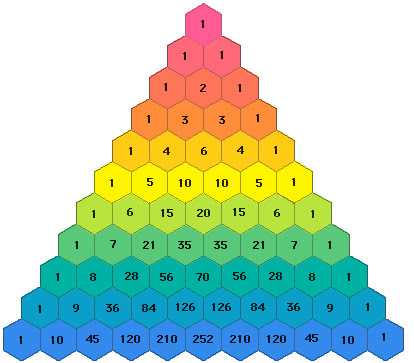
This can be hard to understand, so here we’ll introduce a cute and very useful visualisation, called Pascal’s Triangle. Looking at the image on the right, numbers in the row below come from adding two numbers next to each other, directly above. The ‘2’ in the third row comes from adding 1 and 1 above it. Both 3s in the fourth row come from adding 1 and 2 on either side; the 4s from 1 + 3, and 6 from 3 + 3…
These numbers can give you the binomial coefficient for simple cases like a coin flip. Row two has 1 and 1 – two numbers in total, so 1 chance in 2 of a head, and 1/2 of tails. What about three coins? Look at row three! 1 + 3 + 3 + 1 = 8. Three heads or three tails correspond to the ends – so one chance in eight (1/8). For two heads, or two tails, you have three ways each out of eight – or a 3/8 chance, which is what we calculated – the ‘3’ is the binomial coefficient here. You can check this by considering all the ways you can flip three coins: if H = heads and T = tails, you get HHH, HHT, HTH, THH, TTH, THT, HTT, TTT. Three of these give you two heads.
If you want to know the chance of, say, six heads in ten coin flips, you can look at Pascal’s triangle and figure it out! Or try the binomial formula. (The answer is 210⁄1,024, or 105⁄512 – about 20.51%).
Shiny Charm Rate
Earlier we said that the Shiny rate if you had the Shiny Charm was close to 3⁄4,096 (~1⁄1,365), but this is not quite it (but very close!). How the Shiny Charm works is that the game effectively rolls 3 times for the Shiny chance, stopping if a shiny is found or once the sixth roll occurs. This is close to 3⁄4,096 (0.073242%), but this isn’t quite right, given you still would otherwise have the chance of finding more than one Shiny Pokémon – or never finding one.
We can use the binomial theorem to find the chance of not finding a Shiny Pokémon after six rolls, and then subtracting, as we only care about any other instance. This makes the true rate 0.073223% (after rounding). It’s a minute difference in the end but it’s neat to know all the same, and it can add up when you consider multiple rolls.
At any rate, we are now armed with the binomial formula and basic probability multiplication. Now we can tackle some questions of interest.
Hordes
A Horde is an encounter with five Pokémon at once. This is a new mechanic exclusive to the generation six games, Pokémon X and Y (XY) and Pokémon Omega Ruby and Alpha Sapphire (ORAS).
Chance of one shiny
This is simple – a Horde is simply like encountering 5 Pokémon in a row, just all at once. With the binomial model formula, the chance of finding just one shiny Pokémon in any Horde encounter is 0.12195%.
It is important to note that this is not the same as 5 * (1⁄4,096)! That gives you 0.12207% chance, which is similar but crucially not the same. This is even more important when more encounters come into play.
Chance for two (or more) shiny
What about two shiny Pokémon in the one Horde encounter? Or three, or even all five? Here’s a table with the results:
| Number of shiny Pokémon | Chance |
|---|---|
| 0 | 99.88% |
| 1 | 0.12195% |
| 2 | 0.0005956% |
| 3 | 0.00000001454% |
| 4 | 0.000000000001776% |
| 5 | 0.00000000000000008674% |
How about finding at least one shiny Pokémon in a horde battle? That’s simply 1 – 0.998779892776 = 0.001220107; or 0.12201%.

You can see that the chances get tiny fast. But this doesn’t mean that finding more than one shiny in the same Horde battle has never happened – because it has! In fact, at least one player has encountered three at once. This is because it’s actually not that surprising, if you consider the number of game sales. Nearly 30 million copies have been sold of XY and ORAS. Ignoring cases of people using Horde battles for EV training, we make the assumption that each game results in, say, two Horde battles. That gives 60 million chances to roll the dice… so it’s not surprising that someone has encountered that event. It’s just unlikely that you would be that person!
Shiny Soft Resetting
We continue with a seemingly simple case that only considers making multiple encounters of the same individual Pokémon. This comes up when people want to find a shiny Legendary Pokémon (say a Shiny Dialga in Pokémon Diamond, or shiny Groudon in Omega Ruby/Kyogre in Alpha Sapphire). The idea is simple. Save the game before the fight starts. Battle the Pokémon. If it is shiny, catch it. If it isn’t, reset the game (or ‘soft reset’ – resetting the game without closing it via holding L, R and Start or Select), and battle again. Repeat until shiny.
So how many battles does it take before you ‘should’ find a shiny Legendary? This can be tricky if you fall into expectation traps. Considering the generation 6 case (shiny chance of 1⁄4,096), you shouldn’t expect to have found one by the four thousand and ninety-sixth reset. Remember the note from before!
The simplest way is to calculate the chance of not finding a shiny, and then subtract from 1 (or 100%) and see when that becomes 0.5 or 50% (assuming your ‘luck’ is ‘dead even’). Consider this table:
| Number of encounters | Chance for shiny Pokémon |
|---|---|
| 1 | 0.024% |
| 2 | 0.049% |
| 3 | 0.073% |
| 50 | 1.21% |
| 100 | 2.41% |
| 500 | 11.49% |
| 1000 | 21.66% |
| 2000 | 38.64% |
| 2838 | 49.99% |
| 2839 | 50.00% |
| 4096 | 63.22% |
| 10000 | 91.30% |
In short, if you’re soft-resetting for a shiny, then you are ‘lucky’ if it takes less than 2,839 resets. But you have nearly a 9% chance of needing more than 10,000 resets before you encounter a shiny Pokémon!
The above is without the Shiny Charm, of course. With that item, the sweet spot is 947 soft-resets. That’s a substantial difference!
Masuda Method
You can apply the same method to find out the break-even chance for breeding a Shiny Pokémon through the Masuda Method and with the Shiny Charm. The 355th Egg you hatch will be the point where you can rightfully claim you are unlucky if you haven’t yet hatch that shiny Rowlet.
SOS Battles

Pokémon Sun and Moon (SM) replaced Horde battles with SOS battles, and with it a method to chain for Shiny Pokémon. Sadly we do not know the full details of the chance rates before a chain of 70. For sake of argument let’s assume it remains 1⁄4,096 until then, and becomes 1⁄1,024 after that rate. (With the Shiny Charm, a considerably easier item to obtain in this game compared to others, the chance rate starts at the more palatable ~1⁄1,365, and after a chain of 70 becomes ~1⁄683.)
Like with the above, how long does the chain have to be to expect a Shiny Pokémon assuming a dead even amount of luck? The calculation is similar to above, but now we have to keep in mind that the chance changes after 70. The other consideration is that there is a maximum chain length of 255. After 255 battles, the chances reset again. After that, you need to start again and work your way back up.
| Number of encounters | Chance for one shiny Pokémon |
|---|---|
| 1 | 0.02% |
| 70 | 1.68% |
| 71 | 1.78% |
| 100 | 4.53% |
| 150 | 8.91% |
| 200 | 12.87% |
| 255 | 16.77% |
| 325 | 18.45% |
| 500 | 32.88% |
| 761 | 50.06% |
This is an improvement to regular soft resets. You need to do 740 random battles to have the same chance of finding a Shiny Pokémon as 255 SOS chain battles, and do just under three full chains worth to get a 50% chance at a Shiny (761 battles). This is nearly four times less battles than soft resetting on average!
What if you have the Shiny Charm? After 255 battles the Shiny rate is almost 30%, and for the 50% chance rate for one Shiny, you’ll need to go through 336 SOS battles (less than one-and-a-half full chains).
Again, this calculation assumes the chance doesn’t improve before you reach a chain of 70; this may not be the case. Further research is needed to verify that however, but it does mean the chances could be even better.
The perfect wild Pokémon
Perfect IVs
Let’s now consider you encountering any Pokémon in the wild, or getting a gift Pokémon (e.g. a Starter). What’s the chance that it’s as strong as it can be? We’ll start off with IVs. If you want an Attack IV of 31 (the highest possible), you have a 1⁄32 chance. If you just want any stat to have a perfect IV, you may think it’s 6 * (1⁄32), or 18.75% – this is wrong! If you had 32 stats you can’t be sure of one being perfect – they could all be 0, for instance. The binomial formula instead gives us the chance of 15.998% for at least one stat to be perfect.

What about 6 perfect IVs? This reduces the binomial formula to (1⁄32)6, or a chance of 1⁄1,073,741,824 (0.0000000009313%) – less than one in a billion!
Happily, it isn’t necessarily that bad, as often you don’t care about either the Attack or Special Attack stat. In these cases, the chance of five of the stats being what you want is 1⁄33,554,432 (0.00000002980%).
If your Pokémon is a Legendary in a generation six or seven game, you’re in luck. Three stats are assured of being perfect already, so having all six perfect IVs is merely (1⁄32)3 = 0.0031%.
We’ll continue with the six-perfect-IVs case for a non-Legendary Pokémon. Continue, you say? Well, sadly it’s just the beginning, because…
Perfect Stats
…there’s more to it than IVs! For instance, Nature is also a consideration.
It all depends on how fussy you are. For instance, let’s assume we’re talking about a fast sweeper. A Physical attacker ideally wants Adamant or Jolly, while a Special Attacker Modest or Timid. That’s a 2/25 chance you’d get either one, or a chance of 1⁄13,421,772,800. If you want a specific Nature, then it’s twice as bad; 1⁄26,843,545,600. If you came prepared with the Synchronise trick, then it’s 1 in roughly two billion, but let’s not worry about that.
Ability can matter as well. Sometimes you don’t care about the Ability or there’s only the one Ability a Pokémon can have. And to be fair, you can already change the Ability via an Ability Capsule, but those are expensive. Nonetheless, it’s a 50/50% chance in normal circumstances to a specific regular Ability, so halve the chance from before if you do care.
What about a Hidden Abilities (HA)? After all, you can’t use an Ability Capsule to make a Pokémon’s Ability become a HA. You have a chance of that in Horde battles, and while the exact number isn’t known, this kind person reasoned it is around 5% (1⁄20). It can be as good as 15% if you get a high enough chain in SOS battles, but let’s also assume the 5% chance (chain length of 10-19). So perfect IVs, a specific Nature and the HA in a Horde battle: 1⁄536,870,912,000 (or 0.00000000000186%).
And hey, let’s suppose it’s shiny as well (and you don’t have a Shiny Charm which improves your odds). You’re looking at a chance of 1 in 2,199,023,255,552,000. That’s worse than one in two quadrillion.

Feeling lucky? Try PokéRus. Luckily PokéRus can be passed onto any Pokémon after obtaining it, so this isn’t essential. However, in a few cases gender also matters! Some trainers just want a female Popplio for example. In other cases everyone wants a female Salandit or Combee, as only they can evolve. In such cases, you multiply the chance by another factor depending on the gender ratio for the species, typically 1⁄2 down to 1⁄8!
Perfect stats in Pokémon GO
There’s also the likelihood of finding a perfect (or 100%) Pokémon in Pokémon GO. Luckily you don’t need anywhere near as much luck! There are no Abilities or Natures, and there are only three stats; Stamina (HP), Attack and Defense. These have IVs ranging from 0 to 15. So for one perfect stat the chance is 1⁄16, and for all three it is (1⁄16)3 = 1⁄4092, or 0.02441%. That’s right – that’s the same as the regular shiny chance in the main Pokémon games.
It gets better too. Pokémon hatched from Eggs in Pokémon GO cannot have a stat IV lower than 10! The same goes for Raid Bosses. This means that the chance becomes (1⁄6)3 = 1⁄216 (0.463%). Incidentally, with ‘average’ luck you’d be unlucky to not find a perfect Pokémon after 150 Eggs hatched or Raid Bosses caught in Pokémon GO.
As for the chance of finding a Shiny Pokémon in GO (at time of writing, just Shiny Magikarp)? People are not sure yet of the exact rate. The good people of The Silph Road have estimated to be around 1⁄235, but this is a work in progress. You’ll need 163 caught Magikarp with none of them found to be Shiny to be unlucky if that rate was the true one.
Breeding
Thank goodness that we don’t have to worry about catching Pokémon in the wild! You can breed for high IVs and other stats. The catch is that to improve those chances, you need two Pokémon with high IVs to help out. To start with, we’ll assume you have two perfect Pokémon as the parents.
When breeding in sixth or seventh generation games, three IVs from any parent are passed down to the offspring. You can give a bit of control over this as well. One parent holding the Destiny Knot item increases this to 5 IVs. One of the EV-enhancing items (e.g. Power Brace) forces a specific IV to be passed down as well. An Everstone held by a parent will pass down the Nature of that parent and possibly a Hidden Ability (Female has 80% chance of passing it down no matter the other parent, while male/genderless have 60% chance of passing it down if bred with a Ditto).
Lastly, the Masuda method is a way to breed for shiny Pokémon. If you breed two Pokémon from games of different languages (e.g. English and Japanese), in generation six and seven the game effectively tries ‘six times’ to see if your Pokémon is shiny or not. The chance is around 1⁄683, or 0.1463056% (rather than 6⁄4,096, which gives 0.1466%). (With the Shiny Charm this reduces to 1⁄512, or 0.1953%.) Note that a Pokémon from a US game played in, say, French, will work with the Masuda method and a Pokémon from a US game that was played in a different language.
Chance of Perfect Pokémon in breeding
Let’s get to the numbers.
For just perfect IVs and assuming the optimal Destiny Knot item with perfect parents, you have only one IV left to worry about! Hence the chance is 1⁄32; way better than one in a billion and so!
Of course, realistically you will likely not have perfect parents, and this rapidly complicates the calculation. If one had 6 perfect IVs (e.g. your totally legitimate Japanese 6 IV Ditto) and the other 5 perfect IVs for instance, first you have to consider the chance of it not picking the imperfect IV to pass down. Regardless of if it is picked, you know four other stats will be picked, leaving two remaining; so therefore the chance of the imperfect stat being picked is (½)*(½) [chance of that stat e.g. Attack * chance it comes from the parent with the imperfect stat] = ¼. So hence the chance of all five stats chosen from parents being perfect IVs is ¾.
Then you multiply by the chance of the last stat to be also perfect (1⁄32), and end up with 3 in 128 (2.34%).
What if both parents each had only five perfect IVs? If they have the same imperfect stat, it becomes 1.56%; if they have different stats, that becomes 0.78%. The less perfect IVs the parents have, the smaller the chance becomes. If they have less than five perfect IVs for different stats between each other with the Destiny Knot (or three without), the chance automatically becomes 0.
Let’s assume you want that Hidden Ability with the perfect parents case – multiply by 80% to get 1⁄40 (2.5%).
And Shiny as well? Without Shiny Charm or the Masuda Method, it’s around 0.000610%.
Other Cases
There’s three other notable cases; Hordes, SOS and DexNav (the latter exclusive to ORAS). Here we’ll calculate the chance of perfect IVs, perfect stats assuming you want a Hidden Ability, and that with a Shiny Pokémon.
Hordes
There is no special case for higher IVs or the like with Horde Battles – all that is different is that you get five times at the same chance. This turns the chance of perfect IVs to a measly 0.00000046566% – better than the single case, but not that much better. The chance of getting a desired Nature is 50% for each Pokémon in the Horde if using Synchronise. Hidden Ability is not as clear, but this bit of research suggests 5%. The chance for all that together with Shiny (for that one specific Pokémon) is 0.000000000002842%. Very small, to say the least. Five Pokémon in a row isn’t going to help you much here.
SOS
SOS battles are a bit better, because higher chain numbers gives you perfect IVs. Let’s got for an optimal and simple situation and consider reaching chain number 71 – here you can expect at least 4 perfect IVs, a 15% of a Hidden Ability, and a Shiny chance of 1⁄1,024. Nature remains a 50% chance with a Synchronise trick. Put that altogether, and the chance for a perfect Pokémon is (1⁄32)2 * 0.15 * 0.5⁄1,024= 0.00000715%. Still not great at all, but far better than the Horde scenario.
DexNav
Lastly we have the DexNav. It is the most convoluted, with this handy chart indicating the (rough) chance of 3 perfect IVs (at least) or Hidden Ability. The chance of a Shiny from DexNav is well described (and discovered) by mrnbayoh, who also offers up a calculator for this very aspect.
The chance for six perfect IVs, Nature (via Synchronise) and Hidden Ability in a great setup (search level of 100) is 0.0000004211%. If you are curious, multiple this value by the chance of finding a Shiny from the calculator linked above (e.g. at a search level of 100, the Shiny chance is 1 in 1,064 – total chance becomes 0.0000000003958%). This places DexNav between the SOS and Horde methods for obtaining perfect, shiny Pokémon. Breeding Pokémon remains the best way however.
Closing words
Phew! That’s a lot of statistics to get your head around, but hopefully you now have a better understanding of just how lucky you have to be to get that Shiny Pokémon, or one with perfect stats. If you have a situation you’d like to be explored further, be sure to ask away in the comments!
Edited by ddrox13 and tokyodrift.